【マイクラ備忘録】Java版のアップデートで村人が消滅してしまったときの対処法
むぅんです。お久しぶりです。
久々のブログ更新ですが、今回はちょっとしたマイクラのお話です。
ググっても同じ症状の人がパッと見出てこなかったので、もし同様のことが起こった場合参考になれば幸いです。
症状
Java版を1.14.2から1.17.1にアプデしたら村人がほぼ消滅した!
厳選して確保した村人だけでなく、初期スポーン地点から最も近くにある村に自然発生していた村人等も全滅。かろうじて数人拠点周りの施設内で生き残っているのを確認するも、それ以外は忽然と姿を消した。
幸いアプデ前にバックアップは取ってあったので、そこから検証を進めていくことにする。
(なお、1.17.1ではこれまでアプデ後に旧ワールドを読み込んだ際の「バックアップを取る」「危険性を理解した上で読み込む」の選択肢が出てこなかったのでアプデ時は注意)
検証
あまりに一斉にいなくなった上にアプデ直後に起きた現象のため、ゾンビの襲撃等によるものとは考えづらい。
そこでアプデに原因があると予想し、試しに1.17.1ではなく1.16にアプデするも、やはり村人は消滅。アプデ直前に村人が確かにいることを確認し、村人の目の前でアプデを実行するも見事に消えてしまったので原因はアプデでほぼ確定。
次に、1.14.2から1.15にアプデすると、このときは村人は消滅せず。しかし、1.15から1.17.1に上げると今度は消滅。そこで1.14.2→1.15→1.16→1.17.1と段階を踏んで少しずつアプデすれば消えないと考え実行したところ、無事に村人が消えることなくアプデすることに成功した。

まとめ
一気にバージョンを上げすぎるとワールドに多大な影響を与える恐れがある。そこで、バックアップをしっかり取った上で、少しずつ段階を踏んでアップデートすることを推奨する。
なお、今回はたまたまこの方法でうまくいきましたが、この通りにやってもうまくいかない可能性はあるのでその点は予めご了承ください。
デレステの譜面をOpenCVでデータに起こしてみる
こんばんは、むぅんです。
今回は1年以上前にやったデレステの譜面をOpenCVを用いてデータ化する手法を簡単ではありますが書いていきたいと思います。
これ自体は数年前から構想していたのですが、完璧なタイミングでPERFECTを取り続ける動画の撮影が人力では不可能という点で諦めていました。音ゲーによっては放置(全MISS)でもいけるものもあるかもしれませんが、デレステの場合ロングやスライドは手で取らないとそこから先が消失してしまうためこれも不可能です。
そんな中実装されたデモプレイ機能がまさに待ち望んでいたものだったので、無事に実現することができた次第です。
大まかな流れ
1. デモプレイ機能を用いてプレイ動画をノーツ速度10で撮影
2. 動画を1フレームごとに切り出す
3. あらかじめ用意したノーツアイコンの画像でテンプレートマッチングを行う
4. ノーツが検出されたフレーム数や座標から秒数やノーツの種類を割り出し記録
5. 全て記録し終えたらcsvファイルとして出力
録画環境
今回、録画はiPad Pro 10.5インチ(2017年モデル)で行いました。OSはiPadOS 13.3です。古いOSの場合、音がモノラルでしか録音できませんが、今回のプログラムとは一切関係ないので大丈夫です。
Androidでできるかは不明ですが、60fpsで録画できるならおそらく問題ないと思われます。
これ以降、iPadで録画したものとして話を進めていきます。
デレステは今いる画面によってfpsが変動します。例えば、楽曲のプレイ中は60fpsですが、リザルト画面に以降した直後から30fpsに切り替わります。なお、これは後に詳しく解説しますが、OpenCVの cap.get(cv2.CAP_PROP_FPS) は全く当てになりません。これで取得できるfpsは動画の総フレーム数を動画時間で割っただけのものであり、フレームレートが可変な動画であってもお構いなしに平均値が得られるだけです。たとえ60fpsである楽曲のプレイ画面だけを録画しても、録画を終了する際に起動するコントロールセンターが30fpsなのでどの道60fpsにはなりません。逆に、楽曲のプレイ中はそもそも60fpsから動くことはほぼないのでこの関数でfpsを取得する必要はありません。
テンプレートマッチング
テンプレートマッチングには cv2.matchTemplate() 関数を用います。なお、テンプレートマッチングでは普通画像をグレースケールに変換してから処理を行います。
第3引数ではいくつかあるマッチング方法を指定しますが、ここでは cv2.TM_CCOEFF_NORMED を指定します。これはZNCC(ゼロ平均正規化相互相関)と呼ばれる手法で、返り値は から
までの値を取り、より
に近いほど類似度が高いことを示します。
類似度 は、入力画像の輝度値を
、テンプレート画像の輝度値を
とすると次のように計算できます。なお、テンプレート画像のピクセル数は
で、左上の座標を
、右下の座標を
とします。
この関数で得られた結果を cv2.minMaxLoc() に代入することで、最大類似度やその最大類似度が得られた部分の左上の座標が得られます。
試しに、以下のテンプレート画像を用意します。

これを実際のプレイ画面の画像で検出してみます。検出範囲は で、その範囲内にノーツの一部のみが写り込んだときと端から端までノーツが全て写り込んでいる2パターンで検証します。

まずは一部写り込んでいるほう(下図左側)ですが、最大類似度はわずか と到底テンプレートと一致しているとは言えないような結果でした。下図にはテンプレートと同じ大きさの矩形を最大類似度が得られた座標を基準に描画していますが、まるで違う場所に描画されていることがわかるかと思います(ちなみに左上の座標はこの検出範囲内基準で
でした)。
一方、全て写り込んでいるほう(下図右側)では最大類似度は約 となり、ほぼ一致している部分が存在していたということがわかります。左上の座標は
で、描画された矩形は綺麗にノーツのある部分を指し示していることが見て取れます。矩形の中心座標もバッチリど真ん中ですね。

実際には、次の画像に示した5箇所の範囲内でノーツが通過するのを監視します。ノーツを検出したら、6種類あるノーツのうちどれが通過したかを判断し、通過したフレーム数からおおまかな秒数を測定するという寸法です。

ノーツの種類を分類する
現在、デレステのWIDE譜面にはタップ、ロング、左フリック、右フリック、スライド始点(終点)、スライド中間点の6種類のノーツアイコンがあります。この内のどれが通過した判断するには類似度を比較します。要は1フレームごとに6枚全てのテンプレートと比較し、その中で最も類似度が高かったものをそのノーツの種類と判断するわけです。実際にこれはおおよそうまくいき、例えば正解がタップアイコンの画像に対しタップアイコンのテンプレートを用いてマッチングを行った場合、類似度は限りなく に近くなります。一方、他のテンプレートを用いてマッチングしても基本的に
から
程度に留まります。
は十分に高い値ではありますが、たいていそういうときは正解がさらに高い値を示すので普通は問題ありません。このことから、今回は類似度のいずれかが
を超えたときノーツが通過していると判断し、その中で最大値であったテンプレートを通過しているアイコンとみなします。閾値は割と適当なので、これで上手くいかなければ適当な値に調整してみてください。
一方で、最大値を見るだけでは判断がつかない例外もあります。それがスライド始点とスライド中間点です。これらはただ明るさが異なっているだけで、デザインそのものは同じアイコンです。よって、場合によっては類似度がかなり近くなってしまい、判定に疑問が残る形となってしまいました。そこで「そもそも人間もこれらのアイコンを見分けるときに明るさを用いて判断している」という点に着目し、スライドのどちらかである可能性が高まったときだけ画像の画素全ての輝度値の平均値を比較することで始点か中間点のどちらであるかを判断することにしました。OpenCV上では、グレースケール画像は2次元リストに各ピクセルごとの輝度値を持っているだけなので、Numpyの np.average() などを用いて簡単に平均値を算出できます。
なお、今回ノーツを検出しているのは前述の通り の範囲ですが、ノーツ速度10で録画した場合、ノーツはおおよそ4フレーム写りこみます。稀にフレームごとにノーツの種類が違うものと判定されることもあるので、ここでは保険として最頻値をノーツの種類としています。例えば、3回タップノーツ、1回ロングノーツと判定された場合はタップノーツであったと判断します。
ノーツの始点と終点を判断する
終点は前述の通り、マッチングを行う範囲を5箇所に分けていることから自明ですが、始点はどう判断すれば良いのでしょうか?様々な方法を考えましたが、最終的には 関数を用いることで解決しました。これは
の逆関数
とは似て非なるもので、
が
となるような
を求めているのに対し、
は
直交座標における
の偏角を求める関数です。定義は次の通りです。
この関数を用いて、時刻 に検出されたノーツの座標
と時刻
に検出されたノーツの座標
からノーツが進んでいる角度
を計算し、その値によってノーツがどの始点から終点へ向けて流れているか調べようというのが今回の手法です。
例えば、真ん中(左から順に1~5と番号を振るデレステおなじみの記法での3にあたる終点)に向かって流れてくるノーツを考えます。もし3より左側からノーツが流れているとすると、 となることは自然だと思います(
軸は下向きに正であることに注意してください)。一方、右側からノーツが流れていれば
であるはずです。このように、角度を見れば始点がある程度わかるので、後は各々の始点と終点で角度がだいたい何度くらいになるかを1パターンずつ地道に調べていき、その値に応じて泥臭く場合分けするだけです。
ちなみに、 の何が嬉しいかというと、値域が
であることから、たとえ3から3へ向かって流れてくるようなパターンでもエラーにならないという点です。
となるような
は存在せず、
では「ちょうど角度が
の方向へ向かって進んでいるもの」の検出に不向きなのです。ゲームプログラミングなどにおいて角度の取得はごく一般的なので、どのような角度でも正しく角度を返してくれる
はたびたび利用されています(というより
は滅多なことがない限り使われない気がします)。
ここでも、ノーツの種類同様始点候補が複数あったときは最頻値に基づき一番可能性の高いものを始点とします。
ノーツの流れてきた時刻を計測する
ノーツの流れてきた時刻は経過したフレーム数をもとに算出し、そこからy座標による微調整を行います。フレーム数からでは1/60秒の精度でしか秒数を割り出せませんが、ノーツは画面下部では ] ほどの速さで動いており、これを利用することでさらに42倍の精度を得ることができます。細かな調整は環境によって異なると思うのでここでは省略します。
コマ落ちしてしまったフレームを補完する
ここが今回のプログラムのキモであり、大変苦労した部分になります。フレームごとに動画を観察していけばわかるのですが、2~3分ほど録画した場合10箇所程度、最大で3フレームほどまとめてコマ落ちが生じることがあります。3フレーム程度微々たるものと思われるかもしれませんが、前述した通りノーツの流れてきた時刻は1フレームのさらに1/42、すなわち0.0004秒程度の精度で取得できるため3フレームも抜け落ちてしまっては問題です。事実、Frostに見られるようなスライド中間点が密集したような配置でこの現象が起こると目に見えて譜面データの質が悪くなります。
そこで、これを解消するためにffprobeコマンドを利用し動画ファイルの解析を行います。今回はこちらのサイトを参考にしました。
このコマンドで動画ファイルを解析し、その中のpkt_pts_timeという部分に着目すると、各々のコマの正確な時刻がわかります(単位は秒)。例えば、60fpsの動画から次のような時刻のデータが得られたとします。
…, 60.000000, 60.016666, 60.050000, 60.066666, …
皆さんはこの時刻の不自然な点に気付いたでしょうか?60fpsであるならば1フレームごとに進む時間はおよそ0.016666秒であるはずですが、ここでは60.033333秒にあたるコマが抜け落ちていることがわかります。このように、ffprobeコマンドを用いれば各コマごとの時刻がわかるため、本プログラムではフレーム数を1/60倍したものを秒とする単純な方法ではなく、ffprobeコマンドで得た正確な時刻を利用します。もし運悪くノーツの流れてきた時刻を計測するタイミングのコマが抜け落ちてしまった場合は正確な譜面データが得られませんが、そのようなことはめったに起きないため問題はありません。万一奇跡的にそうなった場合は素直に録画しなおしましょう(録画するたびにコマ落ちする箇所は変わるため2回続けて同じことが起きることはないと言っていいでしょう)。
ただし、このコマンドで動画ファイルの解析を行うのには数十秒から数分程度の時間がかかります。そこはぐっと我慢しましょう。
動画の回転について
さて、ここまでテンプレートマッチングで得られたデータからノーツの情報を取得する方法を書いてきましたが、実は前提となる動画に致命的な欠陥が存在しています。それは、iPad(iOSおよびiPadOS?)でデレステを録画すると、必ず90°または270°回転した状態で保存されるという問題です。
これがなかなか厄介で、各フレームごとに画像を回転させるとなると処理にとんでもない時間がかかるのです。これを何とかする方法はないのか調べても情報が出てこず、自分なりに回避する方法を模索した*1のですが、そもそもデレステに限らず横向きで録画した動画は全て同じような現象が発生することがわかっただけでした。これは自分1人ではどうにもならんと悟ったので何を血迷ったかAppleのサポートに直接電話で問い合わせたのですが、どうやらそれは(おそらく)仕様であるらしく回避の方法はないとのことでした。
完全に八方塞がりとなってしまったため、僕が行き着いた手段は縦向きのままテンプレートマッチングを行うという方法でした。そして、得られた座標を後から回転すれば、回転するデータは数百万分の一となり*2処理にかかる時間が大幅に減少します。*3そればかりか、得られた座標さえ回転してしまえば、以降のプログラムは一切書き換えることなく横向きのまま処理を行うことができるのです。
また、それに合わせテンプレートも次のように回転させます。

あれ?さっき見たテンプレートより細くね?と思われるかもしれませんが、これは極端に密集したスライドでも判定を行えるようにするための工夫です。この程度テンプレートを縮めることで、Frost並に詰まったスライドでも正確に検出できます。
余談ですが、Appleのサポートに問い合わせた日、ちょうど東京へインターンに行っており、宿泊先のホテルがなんと携帯の電波が届かない圏外だったためサポートからの電話が受け取れず迷惑をかけてしまいました。Appleのサポートセンターの方々、その節は大変申し訳ありませんでした。
まとめ
以上が大まかな流れになります。正直ここに書いてない細かな処理は山ほどあるのですが、手が疲れてきたため今回はここまでとします。また書き足りていなかった部分があれば都度追記したいと思います。
ちなみに、得られたデータから譜面画像を出力すると次のような画像が得られます。フリックやスライドの補助線こそない*4ものの、かなり良い結果ではないでしょうか?

Q&A(一部内容が被ってます)
あれ?フリックやスライドの補助線は?
テンプレートマッチングではどうしようもありません。誰か自動で読み取れるような手法を思いついた方は是非とも教えてください。
ノーツ速度10で録画しているわけは?
少しでもマッチングの精度を上げるためです。密度の濃い譜面の場合、速度が低ければノーツ同士が重なり合って正しく識別できない可能性があります。
テンプレート画像細すぎない?なんで?
ノーツ速度を上げることで密集したノーツを回避すると説明しましたが、それでもどうしようもないFrostなどの縦に細かく連なったスライドの対策です。
ノーツを押すところではなくそれより上のほうを見ているのはなぜ?
デモプレイなので正確にノーツを叩いてくれはするものの、「ノーツが消失した」ことを検出するよりも「ノーツが通過した」ことを検出するほうが遥かに楽だからです。上に行けば行くほど(ノーツが発射されてからの時間が短ければ短いほど)時間などの精度は悪くなることが予想されますが、少なくともノーツを叩く瞬間より数フレーム程度手前ならばほぼ影響はありませんでした。
ノーツのアイコンがTYPE3である理由は?
TYPE1や2、その他コラボで追加されたアイコンより区別しやすいアイコンだと判断したためです。普段TYPE6でプレイしているのでできればTYPE6で作りたかったのですが、あいにくこのプログラムを書いていた頃はまだ未実装だったため対応できませんでした。今からテンプレートを差し替えてもいいのですが割と面倒なので…。
ノーツの種類を見分けるのは色を見るのではダメだったの?
そのほうが精度はより良くなると思います。ただ、マッチングをフルカラー画像で行うと処理に時間がかかる他、そもそもグレースケール画像でも誤認識しているものは確認できなかった(複数候補があるときは最頻値を採用する手法において)ため問題ないと判断しています。
【デレステ】ブランのフェス限はどれくらい当てやすくなった?
こんばんは、むぅんです。
シンデレラフェスがノワールとブランに分かれて初めての月末フェス限(ブラン)が始まりましたね。
さて、そんなブランフェスですが、今回よりフェス限の提供割合(以下排出率、確率)が調整されました。

今回は、具体的にどれくらいフェス限が狙いやすくなったのか見ていきたいと思います。なお、今回対象とするのはフェス限が1枚だけ追加された先月と今月のフェスです。2枚追加されたときの排出率は1枚につき0.5%、2枚合わせて1%となり、そのぶん恒常が出る確率が下がります。月1開催かつノワールフェスの登場により今後2枚同時に追加される機会はほぼないとは思いますが、予めご了承ください。
過去のフェスの排出率
今回の排出率を見る前に、まずは過去のフェスの排出率を見ていきましょう。
(表1) 2020年12月フェスのSSRの排出率
| 種類 | 対象枚数 | 1種あたりの排出率 | 合計 | ||
|---|---|---|---|---|---|
| 新規フェス限 | 1 | 0.7500% | 1/133 | 0.750% | 1/133 |
| ピックアップフェス限 | 13 | 0.029% | 1/3467 | 0.375% | 1/267 |
| 非ピックアップフェス限 | 29 | 0.013% | 1/7733 | 0.375% | 1/267 |
| 恒常 | 231 | 0.019% | 1/5133 | 4.500% | 1/22 |
ピックアップフェス限とはVo、Da、Viのうちフェスごとにいずれか1種類選ばれているアピール値に特化したフェス限のことです。普通は新規フェス限と同じ特化となっており、例えばVoリフレインが実装された2020年12月のフェスではVo特化のフェス限が出やすくなっていました。ピックアップフェス限と非ピックアップフェス限の合計排出率はどちらも0.375%なので、VoDaViがどれもほぼ同数であることから、個々のピックアップフェス限は2倍ほど出やすくなっているといえます。
また、表1の値はゲーム内で確認できるものとはわずかに食い違っていますが、これは表示上の都合によりゲーム内での排出率は小数第4位で切り捨てられているためです。数値はこちらを参考にしました。
imascg-slstage-wiki.gamerch.com
ブランフェスの排出率
続いて、今回のフェスの排出率を見ていきたいと思います。
(表2) 2021年1月ブランフェスのSSRの排出率
| 種類 | 対象枚数 | 1種あたりの排出率 | 合計 | ||
|---|---|---|---|---|---|
| 新規フェス限 | 1 | 0.750% | 1/133 | 0.750% | 1/133 |
| ピックアップフェス限 | 14 | 0.063% | 1/1600 | 0.875% | 1/114 |
| 非ピックアップフェス限 | 29 | 0.030% | 1/3314 | 0.875% | 1/114 |
| 恒常 | 234 | 0.015% | 1/6686 | 3.500% | 1/29 |
見ての通り、過去のフェス限の排出率が跳ね上がっています。恒常が1%下がったぶんピックアップされているフェス限とされていないフェス限がそれぞれ0.5%ずつ上がっており、先月までと比較すると2.3倍ほど出やすくなったといえます。
その他データ
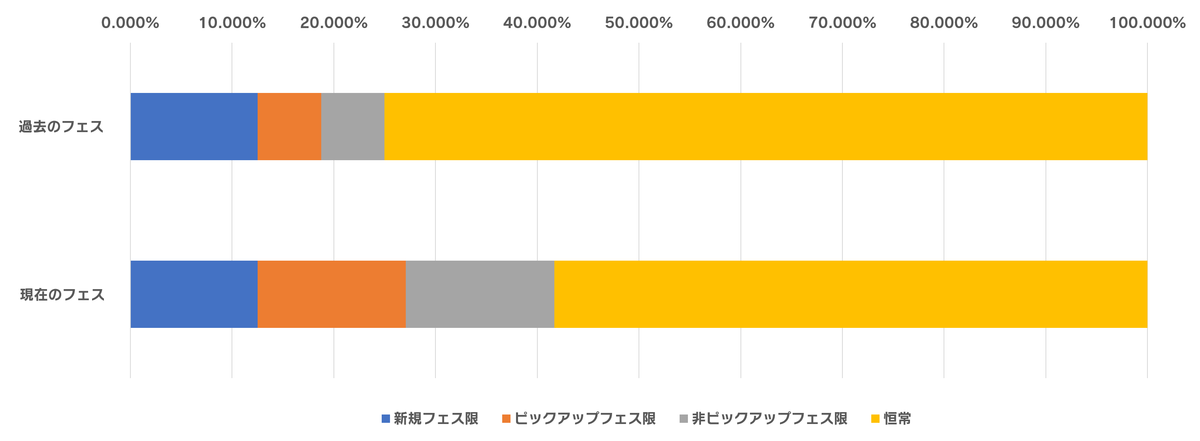
種別ごとの比率は次の通りです。グラフは拡大してご覧ください。
(表3) 種別ごとの比率
| 種類 | 種別ごとの比率 (~2020年12月) |
種別ごとの比率 (2021年1月~) |
||
|---|---|---|---|---|
| 新規フェス限 | 12.500% | 1/8 | 12.500% | 1/8 |
| ピックアップフェス限 | 6.250% | 1/16 | 14.583% | 1/6.9 |
| 非ピックアップフェス限 | 6.250% | 1/16 | 14.583% | 1/6.9 |
| 恒常 | 75.000% | 1/1.3 | 58.333% | 1/1.7 |
また、特技/センター効果別の新規フェス限を含まない排出率は次の通りです。先月と今月が同じ特技持ちのフェス限ならよかったのですが、あいにく先月がリフレイン、今月がシンフォニーと異なる特技でした。ピックアップが与える影響が大きすぎるため、今回はそれらは考慮しないものとします。
ただし、2020年12月のフェスにはリフレインのほたるが入っていないため、完全に同条件というわけではないことに注意してください。
(表4) 2020年12月までのフェスの特技/センター効果別排出率
| Vo | Da | Vi | Cu | Co | Pa | 合計 | |
|---|---|---|---|---|---|---|---|
| 初期トリコ | 1/1244 | 1/2578 | 1/2578 | 1/1828 | 1/1828 | 1/1828 | 1/633 |
| スキブ | 1/1244 | 1/2578 | 1/2578 | 1/1828 | 1/1828 | 1/1828 | 1/633 |
| シナジー | 1/1244 | 1/2578 | 1/2578 | 1/1828 | 1/1828 | 1/1828 | 1/633 |
| モチーフ | 1/1867 | 1/2578 | 1/3867 | 1/3867 | 1/2394 | 1/1828 | 1/846 |
| シンフォ | 1/1867 | 1/3867 | 1/2578 | 1/3867 | 1/2394 | 1/1828 | 1/846 |
| リフレイン | - | - | 1/7733 | - | 1/7733 | - | 1/7733 |
| 合計 | 1/287 | 1/552 | 1/516 | 1/463 | 1/384 | 1/366 | 1/138 |
(表5) 2021年1月からのフェスの特技/センター効果別排出率
| Vo | Da | Vi | Cu | Co | Pa | 合計 | |
|---|---|---|---|---|---|---|---|
| 初期トリコ | 1/533 | 1/1105 | 1/1105 | 1/814 | 1/814 | 1/814 | 1/271 |
| スキブ | 1/533 | 1/1105 | 1/1105 | 1/814 | 1/814 | 1/814 | 1/271 |
| シナジー | 1/533 | 1/1105 | 1/1105 | 1/814 | 1/814 | 1/814 | 1/271 |
| モチーフ | 1/800 | 1/1105 | 1/1657 | 1/1657 | 1/1079 | 1/814 | 1/363 |
| シンフォ | 1/800 | 1/1657 | 1/1105 | 1/1657 | 1/1079 | 1/814 | 1/363 |
| リフレイン | 1/1600 | - | 1/3314 | 1/1600 | 1/3314 | - | 1/1079 |
| 合計 | 1/114 | 1/237 | 1/221 | 1/181 | 1/171 | 1/163 | 1/57 |
この表から、リフレイン以外の特技であれば天井までに1枚くらいは狙ったものが出る程度の確率まで上昇していることがわかります。シナジー等既に9枚出揃っているものは1/300以上とは驚きました…。
まとめ
今回はほぼデータを貼っただけの記事でしたが、属性別の排出率を求めるのは思った以上に面倒でした…(計算ミスがあったらコメントで教えてください)。
流石に一点狙いをするには厳しい確率であることに変わりはありませんが、今後ブランフェスで回す際は以前と比べ遥かに得られる成果はよいものとなるでしょう。
【ポケモンDP】最初に戦うムックルにヒコザルが負ける確率はどれくらい?
こんばんは、むぅんです。
先日Youtubeに投稿されたペレさんによるこちらの動画が大変興味深い内容で、興味本位でヒコザルがムックルに負ける確率を計算したところ、思った以上に反響があったので改めてこちらでまとめてみたいと思います。
動画の結末は本当に面白かったので、まだ視聴されていない方は是非一度ご覧になってみてください。
なお、今回の記事化にあたってはペレさんに許可をいただいております。快く承諾してくださり本当にありがとうございます!
また、一応何度も確認してはいますが、もし計算ミスがあった場合はコメントで教えていただけると幸いです。

ヒコザルがムックルに負ける条件
まずはヒコザルがムックルに負ける条件を整理します。ペレさんによると次の3点を全て満たす必要があります。
① ヒコザルのHPが19であること
ムックルは最大で4ダメージを与えてきますが、最初のこのバトルでは簡単に負けてしまわないようこちらのHPゲージが赤になるとムックルが逃げ出してしまう仕様になっています。赤ゲージとなる条件はHPが20.99%以下となることで*1、ナエトルとポッチャマは例え個体値が最低であってもHPが20以上であることが保証されているため、残りHPが4になった時点でムックルが逃げ出してしまいます。「ならば残りHPを5以上にした状態で次のターンに急所に当ててもらえばよいのでは?」と思われるかもしれませんが、最初のバトルに限ってはそもそも技が急所に当たらないようになっているためこれも不可能です。
したがって、HPが19のヒコザル(残りHPが4になってもまだゲージが黄色)を用意し、次のターンに4ダメージを与えてもらって倒してもらうというのが流れになります。
② 相手が与えてくるダメージが3または4のムックルであること
最大HPが19であるのに残りHPを4にするという話からも分かる通り、ポケモンのダメージは毎ターンランダムに若干変動します。後ほど詳しく解説しますが、ここのムックルは与えるダメージが1または3の個体と3または4の個体の2通りが存在し、後者でないととどめを刺すための4ダメージを与えてくれません。
③ 残りHPが4の状態となり、その次に4ダメージを受けること
前述の通り、ムックルは3または4ダメージのどちらかを与えてきます。残りHPを4にする(合計15ダメージを受ける)ためには「3ダメージを5回」か「3ダメージを1回と4ダメージを3回」のどちらかのパターンを引く必要があります。これも後ほど計算しますが、後者のパターンは滅多に起こりえず、基本的には前者のパターンで残りHPを4にしてから最後に4ダメージを受けて倒してもらうことになります。
ステータスを求める
ここからはステータスを計算していきます。必要なものはムックルの攻撃とヒコザルのHP、防御です。
ステータスの計算式は次の通りです。
HP=(種族値×2+個体値+努力値/4)×レベル/100+レベル+10
それ以外=((種族値×2+個体値+努力値/4)×レベル/100+5)×性格補正
※ただし、小数が出るたび切り捨て
行う計算はたし算、かけ算、わり算だけで大変シンプルなのですが、「小数が出るたびに切り捨て」という処理には注意する必要があります。また、加減乗除の優先順位は通常の計算と同様ですが、かけ算とわり算など優先順位が同一のものは左から順に処理を行います。したがって、例えば「×レベル/100」の部分は「レベルを100で割ったものをかける」のではなく、「レベルをかけた後100で割る」という処理になります。*2
ムックルの攻撃
さて、まずはムックルの攻撃を計算しましょう。種族値は55、努力値は0固定であることからカッコ内の数字は個体値のみに依存し、110(個体値0)から141(個体値31)の間で変動します。ところが、ムックルのLvは2しかなく2をかけた後100で割り5を加えるとその値は確実に7となります。よって、ムックルの攻撃は個体値の影響を一切受けず、最後の計算である性格補正をかける行程でのみステータスが変化するということになります(ここまでの計算で得られた値をここでは補正前のステータスと呼ぶことにします)。性格補正というのは性格によりステータスの一部に得手不得手が生じる補正のことで、1.1、1.0、0.9のいずれかの値を取ります。「いじっぱりのときの攻撃」のように上昇するものは1.1、「ようきのときの特攻」のように下降するものが0.9です。最終的に、小数が出るたび切り捨てルールにより、0.9をかけたときのみ攻撃が1減り6に、それ以外の場合は7のままになります。
以上のことをまとめると以下のようになります。
| 個体値 | 性格↓ | 性格- | 性格↑ |
|---|---|---|---|
| 0~31 | 6 | 7 | 7 |
ヒコザルの防御
続いてヒコザルの防御を計算します。種族値は44であり、ムックルの攻撃同様カッコ内を計算すると88(個体値0)から119(個体値31)の間で変動します。先ほどのムックルと異なり、Lvが5であることからカッコ内が88のときの補正前のステータスは9となるのに対し、カッコ内が119のときは10となります。すなわち、個体値によりステータスが変動するのです。では、補正前のステータスが9から10に上がる境界はどこなのでしょうか?これは次の不等式を解くことで計算できます。
ここで、 は実数
に対して
以下の最大の整数を返す関数です。*3 これを解くと
となり、個体値が12以上のとき補正前のステータスは10となることがわかります。なお、
を満たすとき補正前のステータスは11となりますが、個体値の上限は31であることから実際に11になることはありません。
更に面倒なのが性格補正で、10という値は1.1倍するとちょうど11になり切り捨ての処理を受けないのです。一方、9は1.1倍しても9.9にしかならず、ギリギリ10に届かないため切り捨てられて結局9に戻ってしまいます。このように、ヒコザルの防御は個体値や性格によって様々な値を取ることになり、それらをまとめるとこのようになります。
| 個体値 | 性格↓ | 性格- | 性格↑ |
|---|---|---|---|
| 0~11 | 8 | 9 | 9 |
| 12~31 | 9 | 10 | 11 |
ダメージを求める
続いてダメージ計算を行います。
計算式は次の通りです。
ダメージ=(((攻撃側のレベル×2/5+2)×威力×攻撃/防御)/50+2)×乱数補正/100×タイプ一致補正
※ただし、小数が出るたび切り捨て
これもやはりただの加減乗除の組み合わせでしかないのですが、最後のほうにある乱数補正というのがなかなかに曲者です。乱数補正は85から100までのいずれかの整数を毎回ランダムに取り、これを100で割ることでダメージを最大で元の85%にまでカットするという計算になります。ただ、幸運なことに、ムックルのたいあたり(威力35)では、互いのLvが低すぎるのも相まって乱数補正が100だったときのみダメージが変動せず、それ以外のときは全て小数が出るたび切り捨てルールにより1下がるという何ともわかりやすい結果となっていました。最終的にタイプ一致補正(たいあたりのタイプとムックルのタイプが同じことによる1.5倍のボーナス)がかかる影響でそのダメージ差は2に広がりますが、それでも結果は思ったより綺麗にまとまります(後の計算のため、パターンごとに記号を割り振っています)。
| ムックルの攻撃 | 6 | 7 | ||||||
|---|---|---|---|---|---|---|---|---|
| ヒコザルの防御 | 8 | 9 | 10 | 11 | 8 | 9 | 10 | 11 |
| ダメージ | 3または4 (パターンA) |
1または3 (パターンB) |
3または4 (パターンC) |
1または3 (パターンD) |
||||
確率を計算する
ここまできたら後は確率をひたすら計算するだけです。
② 相手が与えてくるダメージが3または4のムックルである確率
これは先ほどの表でいうところのパターンAまたはパターンCにあたります。これを計算するために、ムックルの攻撃とヒコザルの防御がそれぞれどのくらいの確率でどの値を取るのかを計算する必要があります。
まず、ムックルの攻撃は性格にのみ依存することから、性格がどのように決まるかさえわかれば計算できます。性格は攻撃、防御、特攻、特防、素早さのいずれかが上がり、いずれかが下がることから25通りに分かれていますが、「攻撃が上がって攻撃が下がる」のように互いに打ち消し合うパターンも存在するため、実際にはある特定のステータスが上がる(もしくは下がる)性格は4通り存在することになります。*4 したがって、ムックルの攻撃が下がる性格になる確率は です。補正がかからないときと上がるときも同様に計算でき、結果はこのようになります。
| 個体値 | 性格↓ | 性格- | 性格↑ |
|---|---|---|---|
| 0~31 |
一方ヒコザルの攻撃は性格だけでなく個体値によっても変化するため、計算は中々面倒なことになります。例えば、個体値が11以下で性格に補正がかからないときは
のように確率は両者の積で表されます。これらをそれぞれ計算し表を埋めたものがこちらになります。
| 個体値 | 性格↓ | 性格- | 性格↑ |
|---|---|---|---|
| 0~11 | |||
| 12~31 |
これらの確率から、まずはダメージがパターンAとなる確率を求めていきます。パターンAはムックルの攻撃が6、ヒコザルの防御が8のときなので
となります。一方、パターンCとなるのはムックルの攻撃が7、ヒコザルの防御が8または9のときなので
このどちらかのパターンであれば良いため、②を満たす確率は
です。思ったより高いですね。実際、ペレさんは動画の概要欄で「確率はだいたい半々」と述べられていますが、この計算結果をパーセンテージで表すと約40.86%となり、ペレさんの体感が大きく外れていないことがわかります。流石です。
③ 残りHPが4の状態となり、その次に4ダメージを受ける確率
これは「3ダメージを5回」か「3ダメージを1回と4ダメージを3回」のどちらかを引く確率の和となります。乱数補正が85から100までの16通りである内、ダメージが4となるのは乱数補正で100を引いたときだけであることから、4ダメージを引く確率は です。これより、前者の確率は
とそこそこの高さである一方、後者の確率は
と極めて低い確率となります。両者の和は
となり、4ダメージを2回以上引くパターンはほぼ影響していないことがわかります。このことから、リセットを繰り返しヒコザルが倒される瞬間を見るためには3ダメージを5回引いてから4ダメージを引いて倒されるのを狙うことになりそうです。
まとめ
いかがでしたか?シンプルな問題ながら、思ったより考えることが多かったのではないでしょうか?計算そのものは高校数学で触れる基礎レベルのもののみなのでそこまで難しくはありませんが、数字が結構エグいことになるのでとても手で計算しようと思えるものではありませんね…。
なお、これは余談ですが、ステータスの条件(①②)を満たしている際にヒコザルがムックルに負ける確率は③の4.5319%ほどとなります。これはエアスラを外す確率と大体一緒で、およそ22回に1回は負けてしまう計算になります。したがって、「ヒコザルのHPが19かつムックルから3ダメージを2連続で受ける」など①②の条件が整っていることにうすうす勘付いたとき、もしヒコザルが偶然にも色違いだった場合は速攻で倒しにかかることをオススメします。*5
最後になりますが、ペレさんの動画は面白い検証動画ばかりなのでこの動画で興味を持たれた方は是非他の動画も見てみてください。色違いポケモンが大好きな自分が特に面白かった動画とともに紹介しておきます。
ではまた!
THE VILLAIN'S NIGHTの不正行為によるBANとデレステのスコアタ環境について
こんばんは、むぅんです。
今回は先日話題になった、THE VILLAIN'S NIGHTのイベントにおける不正行為によりサービスの利用停止が実施された(所謂BAN)アカウントの件について書いていこうと思います。

概要
実際に不正行為がどのようなものであったかは、こちらのツイートの画像を見れば一目瞭然です。82位のユニットだけが他とは明らかに異なることが見て取れます。
THE VILLAIN'S NIGHTのハイスコアランキング1位~100位の編成一覧です
— むぅん (@shinemoon227) 2020年10月29日
82位はなぜこれでいけると思ったのか pic.twitter.com/jYT9sAn09c
今回のBANに伴い、ランキング順位の修正が行われました。その結果、イベントptランキングの称号から2000位より上に1人だけその対象者がいることが確認されています。さらに、範囲を全参加者に広げると合計で3人がBANされたようで、恐らくそのうちの1人がこの82位のプロデューサーであったことはほぼ間違いないでしょう。*1
ツイートした経緯について
そもそも、僕がこのような形で1位から100位までの順位を一覧にしたのは他の方のツイートから82位の存在を知ったためで、そのうちの半分くらいが「82位だけおかしいよね」ということを伝えたく、残りの半分くらいが「それはそうと最上位は見事なまでに同じ編成だな」ということを視覚的にわかりやすくまとめてみたかったという目的で作成したものです。82位のユニットとは別に「59位までずっと同じユニットじゃん」という書き込みも各所で見られ、それを自分の目で確かめたかったというのもあります。
このツイート以降、「見てる人はやっぱり見てる」「こんな調査を行ってる人がいればそりゃ不正はバレるよな」との書き込みを見ましたが、自分は普段からそのような調査を行っているわけではありません。ただ、実際に見てる人は見てるというのは間違いありませんし、自分の周辺の人の編成を見ている過程で偶然目に留まることももちろんあると思います。ですので、不正行為はやはりやるもんじゃありません。
結局82位のユニットはおかしいのか?
ここからは「82位のユニットで該当のスコアを取ることは本当にできないのか?」ということを実際に調べていきたいと思います。
見る人が見ればどう考えてもおかしいのは一発でわかるのですが、実際のところ先日公式からアナウンスがあるまでは「82位だけ明らかにおかしいよな」ということを伝えたかったはずが「82位の人すげぇ!!皆似たりよったりのユニットの中1人だけよくこんな編成を思いついたな…」とか「よくスコアタのことを知らない人がたまたまランクインしてるだけで晒すのは可哀想では?」といった意見をそこそこ見かけました。確かに普段からスコアタに興味がある人でなければそう見えるのも不思議ではないので、今一度1つずつ丁寧に見ていきます。
まずは該当者のスコアを見ていきます。

スコアは1989659とのことですが、果たしてこれだけのスコアを取ることは可能なのでしょうか?該当のユニットは次のようになります。


まず、何と言ってもおかしいのが特技発動率に誰1人ポテンシャルを振っておらず、それどころか特技Lvが10ですらないアイドルが複数いることです。5人とも発動率は「高確率」に分類されており、本来特技Lv10かつポテンシャルを最大まで振っていれば特技発動率は100%を超え特技は毎回全発動(全鳴き)します。*2 *3
詳細な計算は省きますが、この場合の特技発動率は左から順に75.11%、78.00%、78.00%、78.00%、66.44%になります(おおよその値です)。曲を通しての特技発動回数は左から順に13回、17回、30回、15回、17回であり、1人あたりの特技全発動率は2.42%、1.46%、0.06%、2.41%、0.10%ほどで、これが5人全員となるとその確率は0.0000000002862690%、分数に直すと1/34932176000というとんでもない低確率になります。仮に1曲クリアするのに3分かかったと仮定すると、全鳴きするまでに(休憩なしで)平均で194000年ほどかかる計算になります。*4
では、このユニットで実際にいくらくらいスコアが出るのでしょうか?今回はデレステ計算機(Ver6.11)を用いて計算を行います。

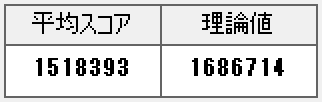
はい。わかりきってはいましたが、このユニットだと平均で151.8万しか出ないようです。何かの奇跡が起き、本当に運良く全鳴きした上でLv30の譜面をコンセントレーションを含んだユニットでAPすることができたとしても168.7万までしか出ません。
一応、理論値を超える方法がないわけではありません。それが巻き込みと呼ばれるテクニックを利用するというものです。これはPERFECTの判定が数フレームに渡ることを利用し、ノーツが判定ラインを超えた後に特技が発動する場所でほんの少しだけ遅めに、判定ラインを超えるより少し前に特技が発動する場所でほんの少しだけ早めに画面を叩くことで無理やり特技をノーツに適用させるテクニックです。実際、1位のスコアは2090092で、これは同編成でAPした際の理論値2089010より1000点ほど高い計算になります。*5
しかし、それを完璧に行える腕があったとしても伸びるのは高々5万点程度です。*6 350億分の1の奇跡を起こすことを度外視したとしても、ただでさえコンセの影響で狭くなっている判定幅の中で微調整を行い、理論値から更に30万点も上乗せするのは不可能と見てよいでしょう。スコアタについて詳しくない人がたまたま取れるようなスコアでは到底ないのです。
この編成自体は決して弱いわけではないのですが(オルタネイトを持っていない場合は十分に良い組み合わせで、金トロ獲得も視野に入るくらいには強い編成です)、THE VILLAIN'S NIGHTのMASTER+はデレステのWIDE譜面としては史上初のロング・フリックの両方が一切存在しない譜面で、アクト系の特技に関していえばスライドアクト以外の相性は最悪です。言い換えるとMASTER+は純粋な物量譜面であったということになりますが、その一方でMASTERはフリックがおよそ46%を占める圧倒的なフリック譜面で、フリックアクトとの相性は抜群だったと言えます。もしかして、この方はMASTER+もフリック譜面だと勘違いし、MASTERで同じユニットを用いてこのスコアを出したのでしょうか…?*7
昨今のスコアタ環境について
さて、今回一番この記事で伝えたかったのはここからになります。それはデレステにおけるスコアタ環境についてです。
実は、このツイートに関連して、「同じユニットばかりで本当につまらんゲームだな」「昔はこんなことなかったのに…」といった書き込みがかなりの数見られました。これは僕にも悪いところはあって、あの画像を見れば誰だって「うわ、ほとんど同じ編成じゃん」と驚くのは間違いないと思います。140字の中で全てを書くのは無理だったにせよ、スコアタに詳しくない人からすれば「82位だけおかしい」という表現は「82位の人だけユニットを工夫してトップ層に入ったすごい人で他の人はつまらん」というふうに繋がってしまうのも無理のないことでしょう。*8
同じユニットばかりが並んでいることについては、デレステの仕様上どうしようもないことだと言えます。デレステのスコアは合計アピール値やノーツ数から求められる基礎値に特技倍率やコンボによるボーナスをかけるという非常にシンプルな式から算出されます。相手と直接戦う格ゲーやターン制コマンドバトルならいざ知らず、デレステのスコアタはユニット、譜面およびプレイヤーの操作方法によりスコアが(確率的に変動するとは言え)決定されるゲームです。極端な話、他者とリアルタイムで読み合いになるようなことはなく、数値を計算機に入力すればポンと結果が出る、そういうゲームなのです。*9
では、どうすれば似たりよったりのユニットでない環境にすることができるのでしょうか?同じ編成ばかりでつまらないという人はここで手を止めて一度考えてみてください。
個人的に思いついたのは次のような方法です。
運要素をマシマシにする
これが一番現実的な案だと思います。例えば、同じアイマスの音ゲーであるミリシタは特技の発動率が特技Lv10でもわずか40%しかなく、更に5凸を行い(同じアイドル同士でなくても構いませんが、デレステでいうところのスターレッスンに近いものです)限界まで強化しても50%どまりです。そのため、運によるスコアのブレがかなり大きく、スコア計算式の違いもあってAPしたときよりコンボを切ったときのほうがスコアが高かった、ということも珍しくないゲームです。
デレステもかつてポテンシャル解放機能がなかった頃の特技発動率は最大80%で、そのときですらスコアの変動が激しくユニットは今ほど完璧に揃っていなかったと記憶しているので、それより更に特技発動率を下げれば上位勢のユニットがバラバラになるのは確実です。
全く同じ性能を持つアイドルを複数出す
これは極論ですが、同じアイドルばかりが並んでいるのが気になるのなら性能が全く同じアイドルを複数出せば少なくとも同じアイコンが並ぶことはなくなります。これはもちろん冗談ではあるのですが、実際にはライパでいつも同じ顔ぶればかりが揃う、センター効果「シンデレラチャーム」持ちのアイドルではこのような意見が出ることはよくあります。ファン活に有利すぎるから、性能面であまりに優遇されているから、特訓前後でユニットに入れざるを得ない今の環境がおかしいから、と理由は様々ですが、確かに同じ性能のアイドルを複数出すこと自体悪くはないのかな、といった感じもします(それが強特技持ちなら)。*10
イベント特効の概念を追加する
モバマスにあるように、そのイベントでだけ特定のアイドルが大幅に強化される仕様を追加すれば、少なくとも毎回「またこのユニットかよ」ということはなくなります。運営が自ら「この編成を使っておけば強いよ」と提示してくれているようなものなので、1つのイベント内だと今以上に同一編成ばかりが並ぶ光景になるのが容易に目に浮かびますが…。
スコアの計算式を複雑怪奇にする
ある程度知識があれば理想編成がわかってしまうのが問題なのであれば、スコアの計算式を今とは比べ物にならないほど複雑にすれば良いのです。それこそ、イベントごとにスコアの計算式を変えてしまえば完璧です。皆手探り状態でイベントが始まるので、最終的には各々違ったユニットを使ってスコアタをすることになるでしょう。
どうでしょうか?個人的には今のデレステではやはりどれも現実的ではないように思えます。*11
スコアが増えるのはノーツを叩いた瞬間なので、楽曲ごとに複数の編成でほとんど同じようなスコアが出るように調整するのも非現実的です。
そしてデレステの環境が昔と変わってしまったということに関しては、正しくもあり間違ってもいると思っています。確かに今のレゾ一強環境は僕としてもやりすぎ感はあると思いますし、オルタネイト環境が整う前からリフレインという新特技の投入により属性曲のスコアタ環境がレゾりあむ、レゾ仁奈のとき以上に一極化してしまったのは早いところ手をうってほしいのは事実です。しかし、その一方でアクトなどの新特技の登場により編成が多様化していることも確かです。かつては(特技発動のブレはさておき理論上は)この編成を持っていれば間違いない、というユニットがガシャ更新ごとに各所で取り上げられ、それが今のトレンドのようになっていた時代がありました。ところが、特技の種類が増えたことにより楽曲ごとに理想編成が異なる形になってしまったが故に、現在ではそのような記事はほとんど見かけなくなりました。
加えて、現環境ではレゾリフ編成が1つの答えとして出てはいるものの、それはゲストありかつ特訓前の編成を前提としており全てのイベントで活用できるわけではありません。というより、アタポン形式、Groove、Parade、Carnivalとイベントがある中でゲストを借りてこれるものは当イベントのようなアタポン形式のみです。特に、Carnivalは同一アイドルの編成そのものができず、また楽曲やユニットの組み合わせが無数に考えられるので、上位勢はおろか誰か1人でも完全に同一の組み合わせであることはまず考えられません。デレステのようなキャラゲー寄りの音ゲーでここまで多様性のあるイベントが開催されるゲームは他にあるのでしょうか?
確かにアタポン形式のイベントに限っては曲次第ではこのように1つの答えが浮き彫りになることがありますが、他のイベントや通常のハイスコアランキングではここまで揃うことはあまりありません(試しに数曲ハイスコアランキングから編成を確認してみてください)。それこそ前述した格ゲーやターン制コマンドバトルのような対戦ゲーですら「キャラの強さランキング」や「結論パ」のようなものが作られるわけですから、それよりもシンプルな計算式から勝敗がつくデレステにおいて多様性を求めることは大変難しいわけです。仮に今の環境トップ編成であるレゾリフ編成を禁止したとしても、どの道次にユニオルタなど別の編成がトップに君臨するだけです。
まとめ
後半からかなり話が脱線してしまいました。この記事の要点は次の通りです。
・不正行為は誰かが見ているのでやめましょう
・デレステのスコアはシンプルな計算式から求められ、明らかにおかしい編成でたまたまトップ100に入るスコアが出るようなことはない
・各アイドルごとに性能差がある以上どうしても「最強」は存在してしまうので、ランキング最上位層の編成が似たりよったりなのは仕方ない
今回はイベント終了直後から82位のスコアがおかしいと話題になっていましたが、そもそも界隈では以前より疑惑のある方だったようです。そのために通報が相次ぎBANされるに至ったと思われますが、お知らせにもあるように運営はBANを行ったことを毎回告知することはないそうです。今回はたまたま直接知ることができましたが、いつそれが行われているかは運営以外には分かりません。スコアを不正に高くして上位に入っても何も良いことはないので、不正行為はやめましょう。
*1:ハイスコアランキングは称号などの後から順位が形として残るものは配布されないので、イベントptランキングで該当者の順位を知っていない限り正確に調査するのは不可能です。
*2:楽曲の属性とアイドルの属性が一致していない場合は80%どまりです。今回のイベント曲はPaで、アイドルも5人全員Paなのでここでは100%になります。
*3:特技が発動することを「鳴く」と呼ぶことがあります。
*4:ポケモンで例えるとハイドロポンプ(命中80)を92連続で当てるようなものです。実際にはいずれも80%に届いていないのでそのレベルですらありません。
*5:正確には、1位の方のポテンシャルを記録していなかったのでVo/Da/特技に10、Viに5振りで計算しています。Pa曲であるにもかかわらずCu属性の桃華が入っている都合上、特技に10振っていたとしても全鳴きの確率は5.5%ほどしかありません。18回に1回程度しか理論値を出せるチャンスがないことに加え、Lv30の高難度譜面で巻き込みを狙いつつAPするのは至難の業であったでしょう。他のイベントでは、1位の方のスコアが理論値より数万点高いこともあります。
*6:もちろん最上位勢からしたら1点でも高いに越したことはないので高々という表現は不適当かもしれませんが…。
*7:デレステでは楽曲Lvごとに異なる係数が設定されており、高Lvであればあるほどスコアが高く出るようになっています。もしかすると「MASTER用のユニットならそっちで88位を取ったんじゃないの?」と思われる方がいるかもしれませんが、いくらフリックアクトが刺さるとは言え、流石にこの編成でMASTERのほうがスコアが高くなることはありません(計算してみると平均値が約141.9万、理論値が約158.3万です)。
*8:本音を言うと画像内に「不正行為の疑い大」とはっきり書いているのでそこまで読んでほしかったですが…。
*9:最上位層はポテンシャルのわずかな配分やまだ未開拓のユニットの模索などといった形で読み合いになることはあります。
*10:特にチャーム(シナジー)に関して特訓前が理想編成入りすることは、ゲームのバランス的にも複数所持していたのに全て特訓させてしまった(重ねてしまった)人的にもよろしくないのでは、と問題視されてきました。先日それはリフレインの特訓前後入りが理想編成となることで解決しました(解決とは)
*11:例で挙げたゲームが悪いということではなく、今のデレステからその方向に持っていくのは難しいという意味です。そもそもスコアの計算方法を変えてしまってはハイスコアランキングやPRPが意味を成さなくなってしまい大問題です。
【2020/07版】プラチナメダルを集めるのにいくらかかるか計算するシミュレータを作ってみた

タイトルの通りです。2年ぶりに最新の仕様に更新してみました。プラチナメダルを任意の枚数集めるまでに大体いくらかかるかを計算してくれます。
実行するたびに結果は変わるので色々試してみてください。
※プログラムが間違っている可能性は十分に考えられるので、使用は自己責任でお願いします。
なお、各SSRの排出率(特にシンデレラフェス)は毎回変わって実装が面倒だったので、ここでは2020年7月20日現在の直近のガシャでシミュレートします。すなわち、シンデレラフェスは2020年6月の「[フレ・デ・ラ・モード] 宮本フレデリカ」、「[やすらぎの温度] 高森藍子」が追加されたガシャ、限定ガシャは2020年7月の「#サマデレ 納涼☆七夕☆夏模様ガシャ」、恒常ガシャは2020年7月の「[栄光へのアーチ] 愛野渚」、「[アモソーロ・ファンタジア] 梅木音葉」が追加されたガシャとなります。
2年前と比較したい方は以下のリンクからどうぞ。
shinemoon227.hatenablog.jp
まず、ガシャの種類を以下から選択します。
【シンデレラフェス】
SSRの確率は6%です。
ピックアップ枠1(0.500% × 2種):
[フレ・デ・ラ・モード] 宮本フレデリカ / [やすらぎの温度] 高森藍子
ピックアップ枠2(0.034% × 11種):
[ワンダーエンターテイナー] 本田未央などの旧Da特化フェス限
ピックアップ枠3(0.015% × 24種):
[ピースフルデイズ] 島村卯月などのその他フェス限
恒常SSR(0.020% × 205種):
[ふんわり和心] 海老原菜帆までの恒常SSR
【限定ガシャ】
SSRの確率は3%です。
ピックアップ枠1(0.400% × 3種):
[#この瞬間を楽しんで] 砂塚あきら / [ほしにねがいを] 遊佐こずえ / [一夜の煌きは永遠に] ナターリア
ピックアップ枠2:
なし
ピックアップ枠3:
なし
恒常SSR(0.009% × 205種):
[ふんわり和心] 海老原菜帆までの恒常SSR
【恒常ガシャ】
SSRの確率は3%です。
ピックアップ枠1(0.750% × 1種):
[栄光へのアーチ] 愛野渚 or [アモソーロ・ファンタジア] 梅木音葉 (いずれか一種)
ピックアップ枠2:
なし
ピックアップ枠3:
なし
恒常SSR(0.010% × 208種):
[ストイック・マイスタイル] 小室千奈美 / [純朴の若草] 奥山沙織までの恒常SSR
次に、下のテキストボックスに目標のプラチナメダルと今現在自分が持っているSSRの種類を入力します。ここの数字を増やすと、最初からある程度アルバムが埋まっていることになるので早くプラチナメダルが貯まりやすくなります。
それぞれ入力できる最大値は次のようになります。
| シンデレラフェス | 限定ガシャ | 恒常ガシャ | |
|---|---|---|---|
| ピックアップ枠1 | 2 | 3 | 1 |
| ピックアップ枠2 | 11 | 0 | 0 |
| ピックアップ枠3 | 24 | 0 | 0 |
| 恒常ガシャ | 205 | 205 | 208 |
また、プラチナメダルは1000枚まで目標として設定できます。
最後に、詳細を表示するかどうかチェックを入れます。ただし、詳細は非常に長いのでプラチナメダル200枚以下のときのみ表示できます。
なお、ここでかかる金額は最も1個あたりの価格が安いスタージュエルG(1個あたり7/6円)で計算しています。現在では毎月3回これより更に安いスタージュエルを購入できますが、購入制限があることを踏まえここでは考慮していません。
Torch Tower(常盤橋プロジェクトB棟)は世界一巨大な超高層建築物か?
こんにちは、むぅんです。
今回は普段の投稿とまったく異なる話題ですが、前々から記事にしたかったことについてです。
【2020/9/18追記】名称およびデザインの変更について一部追記しました。
常盤橋プロジェクトについて
常盤橋プロジェクトは、東京都千代田区大手町と中央区八重洲に4棟からなる超高層ビル群を建設する一大プロジェクトです。
現在これらの建物はA棟からD棟の仮称で呼ばれていますが、その中のB棟は現在日本で最も高い超高層建築物であるあべのハルカス(高さ300m)を有に超える390mという高さで建築される予定であることから日本中で注目されている計画となります。
【2020/9/18追記】常盤橋プロジェクトにより開発される街区の名称がTOKYO TORCHとなることが三菱地所より発表されました。同時に、A棟の名称は常盤橋タワー、B棟の名称はTorch Towerとなるようです。この記事では以降の名称を差し替えておりません。あらかじめご了承ください。
また、"Torch"(松明)の名称の通り、B棟は松明をイメージしたデザインに大きく変更されました。よって、下図を最新のものに変更しました。

真ん中にあるひときわ大きな建物がB棟になります。その左側にある建物はA棟で、高さは212mです。
この画像の恐ろしいところは、隣の小さく見えるA棟は現在日本有数のビル群であり常盤橋プロジェクトの計画地でもある大手町・八重洲エリアに竣工済みのいかなる建物よりも高い点にあります。隣に日本一高いビルがあるため相対的に低く見えますが、A棟が既にこのエリアで最も高いと聞くとまるで何かのバグみたいです(この近辺で次点で高いのは隣接する丸の内にあるグラントウキョウノースタワー・サウスタワーの204.9mになります)。
話をB棟に戻します。高さに注目しても勿論凄いのですが、その延床面積はもっとすさまじいことになっています。延床面積というのはその建物の床の面積をすべて足し合わせたものです(バルコニーの一部や吹き抜けなど含まれない部分もありますが詳細な定義はここでは触れません)。建物の大きさを純粋に比較すること(正確な容積を調べること)は困難ですが、延床面積を見ることである程度その建物の大きさをイメージできるため一般的によく用いられる指標です。もちろん、正確な大きさを比較できるわけではないのですが、ここでは「広さ」と「大きさ」という用語を併用することをあらかじめご了承ください。
B棟の延床面積は何と1棟で490,000m²です。これがどれくらいすさまじいのかイメージが湧きにくいと思いますが、具体的な例を挙げると、世界一高い建築物であるドバイのブルジュ・ハリファ(高さ828.9m)の延床面積は464,511m²です。つまり、B棟は世界一高い建築物よりも延床面積が広いのです。
ここで一つ疑問が生じます。
「あれ、もしかして常盤橋プロジェクトB棟は世界一延床面積が広い建築物なのでは?」
そう思いいつか具体的に調べてみようと思っていたのですが、本日目を疑うようなニュースが目に飛び込んできました。
B棟の延床面積が変更される
https://www.kensetsunews.com/archives/461165www.kensetsunews.com
なんと、B棟の延床面積が上方修正されることになったのです。その広さは、驚異の545,000m²です。既に信じられないくらい巨大な建築物であったのに、そこから更に55,000m²も上乗せされることとなったのです。ちなみに、55,000m²というのは国会議事堂(53,464m²)とほぼ同じ広さです。国会議事堂も決して小さくはないのですが、B棟の10%ほどしかないと聞くとやはり頭がバグりそうですね。スケールがまるで違います。
なお、高さに変更はなく、またフロアの数も大きく変わったわけではない(地上61階・地下5階から地上63階・地下4階)ことから、デザインに何かしら変更があると踏んでいます。せっかくなら400mを目指してほしかったところですが、まだ着工されたわけではないため今後さらなる上方修正に期待したいと思います。
【2020/09/18追記】予想通り、デザインが大きく変更されることとなりました。また、その後のリリースでTorch Tower(B棟)の延床面積がわずかに減少し544,000m²となることが判明しました。(https://www.kantei.go.jp/jp/singi/tiiki/kokusentoc/tokyoken/tokyotoshisaisei/dai18/shiryou1.pdf)
かつて世界一巨大だった建築物
さて、皆さんはアブラージュ・アル・ベイト・タワーズという建築物をご存知でしょうか?サウジアラビアのメッカにある尖塔高601mの超高層建築物で、現在世界で3番目の高さを誇ります。

この建築物の延床面積は1,575,815m²です。バケモンか?
しかし、この数字にはちょっとしたからくりがあり、アブラージュ・アル・ベイト・タワーズというのは7棟からなる複合ビルなのです。これをすべてがくっついた単一のビルとみなすか7棟別々のビルとみなすかは明確な定義もないため決めることは難しいのですが、これを単一とするとこれ以上話が進まなくなるのでここでは別々のものとします(本音を言うと、個々は完全に独立しているわけではなく下でくっついているっぽいので単一とみなしても良いと思います。というか、最も高いホテル棟だけの延床面積を調べても全然出てこない(=全部くっついて一つとみなされてる?)のでぶっちゃけ多分これが一番広いと思います)。
現在、世界で最も延床面積の大きな建築物は、中国の成都市にある新世界環球中心です。その延床面積は1,700,000m²とインフレが止まりませんが、これは幅400m、奥行き500m*1とひたすら横に広い建築物であり、超高層建築物ではありません(どこから超高層建築物と呼ぶかといった定義はありませんが、日本では100m、イギリスでは150mとされている事例があるようです。いずれにせよ、一般の人が想像する「ビル」の形とはまるで異なるものです)。

現在、この規模の超高層建築物は計画すらされておらず、「最も延床面積の大きい超高層建築物」はアブラージュ・アル・ベイト・タワーズで間違いないでしょう。では、「複数のビルが連なった複合ビルを除いた超高層建築物で最も延床面積が大きい」ものはどうでしょうか?
この世にあるすべての超高層建築物の延床面積を調べるのは不可能なので、ここではWikipediaの記事にある「350m以上の超高層建築物」に限定して調べてみたいと思います。特に注釈がないものはいずれもWikipediaの日本語または英語の記事に掲載されている値です。
高さが350m以上の超高層建築物の延床面積リスト(2020年6月現在)
※表はスクロール可能です。表が大きいためPCからご覧の方は操作が難しいと思いますが、ドラッグをご利用いただくと若干見やすくなります。
| 延床面積の順位 | 高さの順位 | ビル名 | 都市 | 高さ[m] | 延床面積[m²] | 注釈 |
|---|---|---|---|---|---|---|
| 1 | 3 | アブラージュ・アル・ベイト・タワーズホテル棟 | メッカ | 601 m | 1,575,815 m² | 7棟の合計 |
| 2 | 41 | 深業上城 | 深圳 | 388.1 m | 895,700 m² | 4棟+αの合計*2 |
| 3 | 18 | 長沙IFSタワーT1 | 長沙 | 452.1 m | 725,000 m² | 2棟+αの合計*3 |
| 4 | 36 | 海雲台LCTザ・シャープ・ランドマーク・タワー | 釜山 | 411.6 m | 660,077 m² | 3棟の合計 |
| 5 | 1 | ブルジュ・ハリファ | ドバイ | 828 m | 464,511 m² | 世界一高いビル |
| 6 | 22 | The Exchange 106 | クアラルンプール | 445 m | 453,835 m² | |
| 7 | 25 | 広州国際金融センター(広州西塔) | 広州 | 440.2 m | 448,000 m² | |
| 8 | 10 | 中国尊 | 北京 | 528 m | 427,000 m² | |
| 9 | 50= | フェデレーション・タワー(東棟) | モスクワ | 374 m | 423,000 m² | |
| 10 | 46= | フォーラム66 1 | 瀋陽 | 384 m | 420,000 m² | |
| 11 | 11 | ウィリス・タワー(旧シアーズ・タワー) | シカゴ | 527.3 m | 418,064 m² | |
| 12 | 12 | 台北101 | 台北 | 509.2 m | 412,500 m² | |
| 13 | 8= | CTF金融センター(広州東塔) | 広州 | 530 m | 398,000 m² | |
| 14 | 4 | 平安国際金融中心 | 深圳 | 600 m | 385,918 m² | |
| 15 | 13 | 上海ワールド・フィナンシャル・センター | 上海 | 492 m | 381,600 m² | *4 |
| 16 | 2 | 上海中心 | 上海 | 632 m | 380,000 m² | |
| 17 | 5 | 高銀金融117 | 天津 | 597 m | 370,000 m² | |
| 18 | 20= | 蘇州国際金融センター | 蘇州 | 450 m | 368,000 m² | *5 |
| 19 | 19 | ペトロナスツインタワー(2棟) | クアラルンプール | 452 m | 360,750 m² | 2棟の合計*6 |
| 20 | 6 | ロッテワールドタワー | ソウル | 555 m | 327,137 m² | *7 |
| 21 | 26 | 武漢センター | 武漢 | 438 m | 321,400 m² | |
| 22 | 58 | JW・マリオット・マーキス・ドバイ・ホテル(2棟) | ドバイ | 355 m | 320,314 m² | 2棟の合計 |
| 23 | 63= | 西安国瑞国際金融中心 | 西安 | 350 m | 289,978 m² | |
| 24 | 32 | ジンマオタワー(金茂大厦) | 上海 | 421 m | 289,500 m² | |
| 25 | 46= | 信興広場 | 深圳 | 384 m | 273,349 m² | |
| 26 | 39 | 中国華潤大廈 | 深圳 | 392.5 m | 268,713 m² | |
| 27 | 14 | 環球貿易広場(ICC) | 香港 | 484 m | 262,176 m² | |
| 28 | 17 | ジョン・ハンコック・センター | シカゴ | 457.2 m | 260,126 m² | |
| 29 | 23 | エンパイア・ステート・ビルディング | ニューヨーク | 443.2 m | 257,221 m² | |
| 30 | 8= | 天津CTF金融センター | 天津 | 530 m | 252,144 m² | |
| 31 | 60 | OKO | モスクワ | 354 m | 249,600 m² | |
| 32= | 7 | 1 ワールドトレードセンター | ニューヨーク | 541 m | 240,000 m² | |
| 32= | 31 | トランプ・インターナショナル・ホテル&タワー | シカゴ | 423.4 m | 240,000 m² | |
| 32= | 43 | 30ハドソン・ヤード | ニューヨーク | 386.6 m | 240,000 m² | |
| 35 | 24 | 京基100 | 深圳 | 442 m | 220,000 m² | |
| 36 | 40 | CITICプラザ(中信広場) | 広州 | 391.1 m | 205,239 m² | |
| 37 | 15 | ランドマーク81 | ホーチミン | 469 m | 205,000 m² | |
| 38 | 55 | バンク・オブ・アメリカ・タワー | ニューヨーク | 365.8 m | 200,000 m² | |
| 39 | 33 | 国際金融中心 (香港) | 香港 | 415.8 m | 185,805 m² | |
| 40 | 45 | キャピタル・マーケット・オーソリティ本部ビル | リヤド | 385 m | 185,000 m² | *8 |
| 41 | 50= | セントラルプラザ | 香港 | 374 m | 172,798 m² | |
| 42 | 34 | プリンセス・タワー | ドバイ | 414 m | 171,175 m² | |
| 43 | 16 | ラフタ・センター | サンクトペテルブルク | 462 m | 170,000 m² | *9 |
| 44 | 28 | ワン・ヴァンダービルト | ニューヨーク | 427 m | 162,600 m² | |
| 45 | 57 | アルマスタワー | ドバイ | 363 m | 160,000 m² | |
| 46 | 30 | マリーナ101 | ドバイ | 425 m | 153,920 m² | |
| 47 | 49 | エリートレジデンス | ドバイ | 381 m | 140,013 m² | |
| 48 | 38 | 23マリーナ | ドバイ | 395 m | 139,544 m² | |
| 49 | 20= | 紫峰タワー | 南京 | 450 m | 137,529 m² | |
| 50 | 54 | 中国銀行タワー | 香港 | 367 m | 135,000 m² | |
| 51 | 56 | ビスタタワー | シカゴ | 365 m | 131,400 m² | |
| 52 | 62 | ザ・ピナクル | 広州 | 350.3 m | 118,452 m² | |
| 53= | 37 | 華潤大厦A座 | 南寧 | 403 m | 100,000 m² | *10 |
| 53= | 59 | エミレーツ・オフィス・タワー | ドバイ | 354.6 m | 100,000 m² | |
| 55 | 35 | アル・ハムラ・タワー | クウェートシティ | 414 m | 98,000 m² | |
| 56 | 42 | イートン・プレース大連 | 大連 | 388 m | 62,300 m² | *11 |
| 57 | 29 | 432 パーク・アベニュー | ニューヨーク | 425.5 m | 38,335 m² | |
| 58 | 27 | 111 西57丁目(ステインウェイ・タワー) | ニューヨーク | 435 m | 29,357 m² | 世界一細いビル |
| 59= | 44 | ローガン・センチュリー・センター | 南寧 | 386 m | 不明 | |
| 59= | 48 | セントラル・マーケット | アブダビ | 382 m | 不明 | |
| 59= | 52 | 大連国際貿易センター | 大連 | 370.1 m | 不明 | |
| 59= | 53 | ザ・アドレス・ザ・BLVD | ドバイ | 368 m | 不明 | |
| 59= | 61 | フォーラム66 2 | 瀋陽 | 351 m | 不明 | |
| 59= | 63= | 漢京中心 | 深圳 | 350 m | 不明 |
見ての通り、常盤橋B棟より広い超高層建築物はいずれも複数のビルからなる建物だということがわかります。これはやはりB棟が世界一の座に輝くのか!?
上海中心は本当に380,000m²?
しかし、世界で2番目に高い上海中心の公式ホームページには、以下のように書かれています。
“上海中心”位于中国上海浦东陆家嘴金融贸易区核心区,是一幢集商务、办公、酒店、商业、娱乐、观光等功能的超高层建筑,建筑总高度632米,地上127层,地下5层,总建筑面积57.8万平方米,其中地上41万平方米,地下16.8万平方米,基地面积30368平方米,绿化率33%,“上海中心”是目前已建成项目中中国第一、世界第二高楼。
この情報によると、上海中心は地上こそ410,000m²とB棟よりもやや小規模なものの、168,000m²もある地下空間を合わせると578,000m²となり、わずかではありますが上方修正されたB棟より更に規模が大きいということになります。
地下空間をどう考慮するか?
上海中心は、127階もある地上部分に対し地下はわずか5階しかないにもかかわらず168,000m²という広大な床面積を有していることから、かなりの規模の地下空間であることが伺えます。どんな形であれ、その施設の一部であるなら延床面積に含まれるのは当然ですが、「ビルの巨大さ」を測る上ではまた違った話になってきます。
もちろん上海中心の地下空間を認めないとすると、B棟の地下空間の延床面積も同様に全体から引かなければなりません。上海中心ほどではないにしろ、地上63階・地下4階という地下が占める割合は決して大きなものではありませんが、こちらも地下が階数から想像できる以上に広い可能性もあり、ランキングに大きく関わることも考えられます。
更に、それ以外のすべての建築物の地下も同様に考えなくてはなりませんが、当然その作業は単純に延床面積を調べる以上にコストがかかる(そもそも地上と地下で分けて延床面積が公開されている可能性は低い)ことからもやはり現実的ではありません。そもそもWikipediaには380,000m²という公式が示した地上部分の延床面積ですらない値が掲載されていたことからも、その延床面積の正しさや、地下を含むか否かなどの正確性に欠けることもわかります。世界共通の基準である高さと異なり、各国で異なる基準により計測された延床面積を同列に語ること自体間違ったことなのかもしれませんね。
したがって、ここでは延床面積を見ることで容積がわからずともある程度建築物の大きさを知ることは可能だが、それには限界があると結論づけます。
結論
常盤橋プロジェクトB棟は計画段階で延床面積545,000m²を誇る世界最大級の超高層建築物。ただし、地下を含むと578,000m²の上海中心のほうが更に広い。
加えて、複数のビルからなる超高層建築物を含めるとアブラージュ・アル・ベイト・タワーズが世界一(7棟の合計で1,575,815m²)である。
あとがき
いやー、めちゃくちゃ疲れました。Wikipediaならだいたいのことは載っているだろうと高をくくっていましたが、蓋を開けてみれば延床面積に関する情報は多くの記事で欠けており、しかも日本語・英語・中国語を駆使してググれば割と情報が出てくるという…。恐らくこんなに「平方米(中国語の平方メートル・m²)」でググる機会もそうないと思います。
もちろんこの情報が全て正しいとは限りませんし、もっと色々調べたほうが良かった気もしますが今回はこれで勘弁してください。もし脚注のリンク先の情報が正しいなら、誰かWikipediaの記事に追加しておいてくれると嬉しいです…。
そもそもこの記事を書こうと思ったきっかけは、ネット上の様々な場所で「日本のビルは低すぎる」「世界に遅れている」などと言われているのを度々目にすることからでした。確かに日本は様々な要因により世界に肩を並べるような高さのビルはほとんどありません。特に300mを超える「スーパートール」と呼ばれる超高層建築物は、竣工済みのものであべのハルカスの1棟のみ、今後予定されているものも常盤橋B棟を含めたったの2棟です。
しかし、日本のビルは世界に類を見ないほど巨大です。というより、圧倒的に太いといったほうが正しいかもしれません。当然どのようなビルをかっこいいと思うかは人それぞれですし、世界にある細くひたすら縦に長いビルも魅力的ですが、日本のビルはとにかく1棟1棟が圧巻のインパクトなのです。高さでは負けていても、大きさでは十分世界トップレベルだということを少しでも知っていただけたらと思います。B棟だけでは不十分なので、後におまけとして日本のビルの記事も上げようと思っています。そちらも合わせてご覧いただけたら幸いです。
また、情報の間違いに気付かれた方、延床面積不明となっているところの広さをご存じの方、そして何よりもっと大きな建築物をご存じの方は是非コメント欄で教えていただけると助かります。それでは。
*1:"世界最大の単体建造物に賛否両論、中国", https://www.afpbb.com/articles/-/2955702
*2:"深業上城 - 深圳控股有限公司 深圳項目", http://www.shenzheninvestment.com/c/projects_artical_11.php
*3:"Changsha IFS", https://www.wongtung.com/en/projects/changsha-international-finance-square/
*4:"「上海環球金融中心」(上海ワールドフィナンシャルセンター)始動 ~上海の新たな金融・情報発信の中心、グローバルマグネット誕生~", https://www.mori.co.jp/company/press/release/2008/08/20080828120000000410.html
*5:"江蘇で最も高いビルである蘇州国際金融センターへの最終的な美化工事が行われ", http://www.sipac.gov.cn/japanese/categoryreport/InfrastructureEcology/201706/t20170616_575262.htm
*6:"ペトロナスツインタワー", http://toolbiru.web.fc2.com/cj4n/d-data-k1.htm
*7:"スターツコリア 不動産情報2016年12月号", https://www.starts.co.jp/cmsdesigner/data/entry/korea_report_pdf/korea_report_pdf.00073.00000001.pdf
*8:"PUBLIC INVESTMENT FUND (PIF) TOWER", https://omrania.com/project/capital-market-authority-headquarters/
*9:"TROSIFOL CASE STUDY ヨーロッパで最も高いビルがトロシフォルを採用", https://www.trosifol.com/fileadmin/user_upload/laminated_news/laktha_tower/Lakhta_Tower_JP.pdf
*10:"每日頭條 南山科技園 華潤置地大廈D座 5A甲級寫字樓物業", https://kknews.cc/house/8xv49bq.html
*11:"大连中心·裕景_百度百科", https://baike.baidu.com/item/%E5%A4%A7%E8%BF%9E%E4%B8%AD%E5%BF%83%C2%B7%E8%A3%95%E6%99%AF/5220235?noadapt=1